This two-part series looks at the underlying mathematical theory and practical steps required to execute a spectral analysis of acquired electroencephalographic data. Spectral analysis, analysing how a signal’s power is distributed across a range of discrete frequencies, is fundamental to understanding an electroencephalogram as well as associated changes in psychological states. Solid, robust, replicable electrophysiology is built on the foundation of spectral analysis and one cannot emphasise enough the importance of the Fourier transform in this regard. The first part of this series deals with the general theory of the discrete Fourier transform (DFT), while the second part focuses on the mathematical/statistical properties of an EEG and how to apply a DFT in the context of biomedical signal-processing.
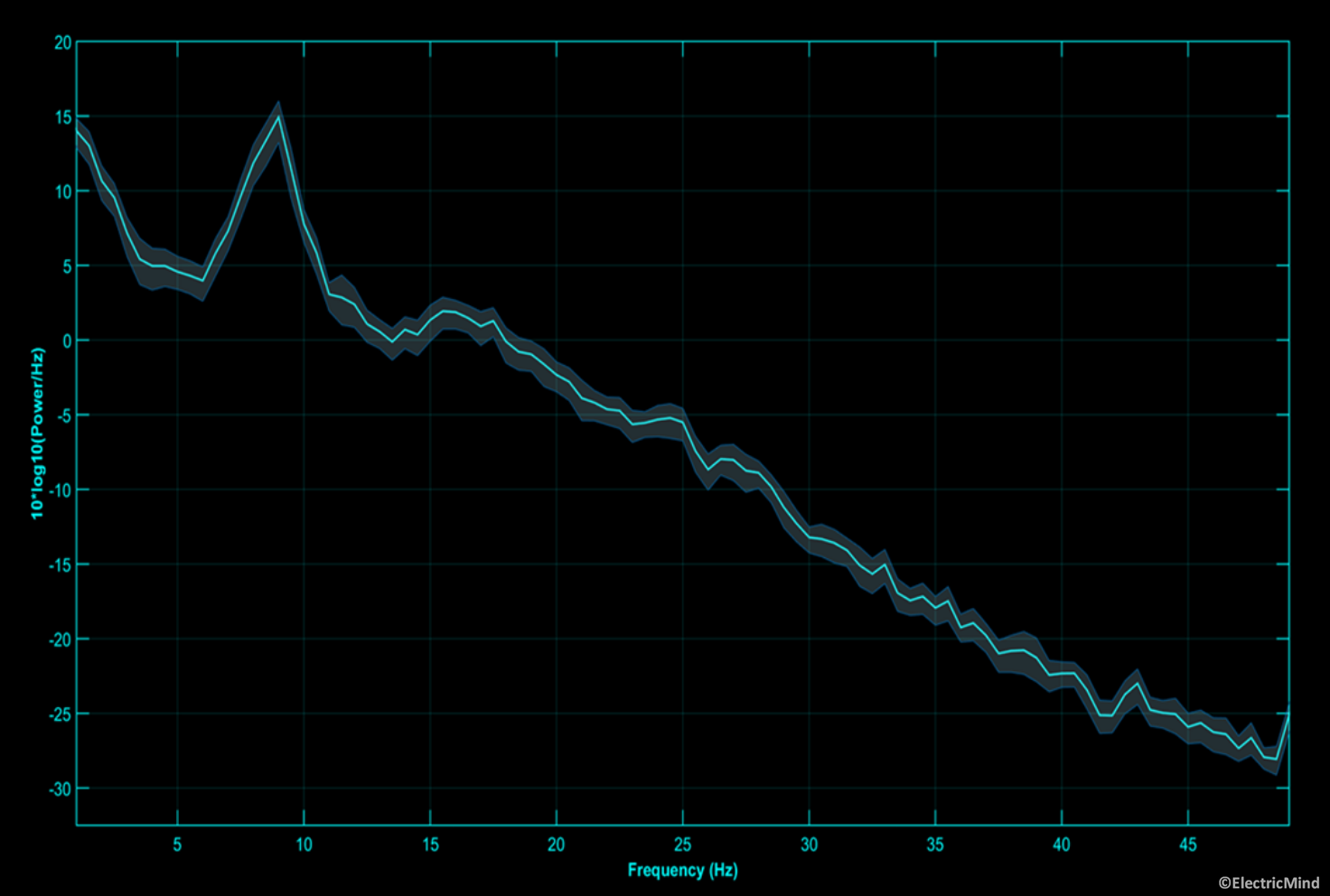
Power spectral density of an electroencephalographic signal recorded over the occipital region during an eyes-open session. The shaded area around the spectrum is the 95% confidence interval around the mean of the estimate. The spectra has a number of prominent rhythmic components. The strong peak at 9Hz is the dominant alpha rhythm. One can also observe a strong beta component from 13Hz-17Hz. Together, these spectral features indicate that the person is alert, awake, and aware of their environment.
The software used for this two-part series is available for download here. The documentation for the software may be viewed here.
The Electroencephalogram, Random processes and the Power Spectral Density
EEG signals are seen as arising from random or stochastic processes, which means the observed/acquired signal, ![]() , at any
, at any ![]() is determined by a unique underlying probability distribution and is related across time by joint probability distributions (Oppenheim & Schafer, 2010, p. 1067-1068). For a random process, the power spectral density (PSD) is theoretically derived by taking the DFT of the autocorrelation sequence of the signal; however, in practical signal-processing, we can use the periodogram as an estimate of the PSD. Both methods are acceptable for purposes spectral estimation of random processes (ibid. Ch 10).
is determined by a unique underlying probability distribution and is related across time by joint probability distributions (Oppenheim & Schafer, 2010, p. 1067-1068). For a random process, the power spectral density (PSD) is theoretically derived by taking the DFT of the autocorrelation sequence of the signal; however, in practical signal-processing, we can use the periodogram as an estimate of the PSD. Both methods are acceptable for purposes spectral estimation of random processes (ibid. Ch 10).
A signal generated by a random process is referred to as a realisation of that process. We may acquire multiple realisations of a given process during a single EEG recording. For analytical purposes, the acquired signal will be segmented into equal length segments—also referred to as epochs. For EEG signals, the segment length can be 0.5 – 2.5 seconds. Enforcing a segment length also ensures stationarity of the segment. Essentially, this means that the signal’s properties, likes its frequency content and amplitude, don’t change over time. In the context of random processes in general, and EEG signal-processing specifically, wide-sense stationarity is a requirement for application of the DFT to a signal or segment. Specifically, time-invariant spectral properties of the signal have a correspondence in relation to its statistical properties, such that:
- the mean of the signal
![Rendered by QuickLaTeX.com x[n]](https://electricmind.me/wp-content/ql-cache/quicklatex.com-94ce5deda23062dfdb5271c8c1471399_l3.png) is time-invariant;
is time-invariant; - the autocovariance sequence is
![Rendered by QuickLaTeX.com x[n]](https://electricmind.me/wp-content/ql-cache/quicklatex.com-94ce5deda23062dfdb5271c8c1471399_l3.png) time-invariant, and
time-invariant, and - the variance of
![Rendered by QuickLaTeX.com x[n]](https://electricmind.me/wp-content/ql-cache/quicklatex.com-94ce5deda23062dfdb5271c8c1471399_l3.png) is finite across time points.
is finite across time points.
Enforcing a fixed length onto signal segments will also affect the lower bound of the analytical band-width, as at least one cycle of the lowest frequency would need to be represented in a segment to be amenable to analysis.
In EEG analysis, and in the analysis of most real-valued random signals, we often scale the power spectral estimate as the distribution of power in the frequency domain per unit frequency: Power/Hertz ![]() , this scaled spectrum is specifically referred to as a power spectral density (PSD). In essence, it is a periodogram estimate; however, the scaling and normalisation applied differ from Eq 8. This is explained further in the following section.
, this scaled spectrum is specifically referred to as a power spectral density (PSD). In essence, it is a periodogram estimate; however, the scaling and normalisation applied differ from Eq 8. This is explained further in the following section.
Truncating and Scaling the PSD
Practically speaking, we are only interested in the values within the range from 0Hz – Nyquist frequency, where the Nyquist frequency is defined as half the sampling rate of the acquired data and is expressed in Hertz. As mentioned previously, the periodogram will provide spectral estimates up to and including the sampling rate of the data. Thus, if the sampling rate was 128Hz, we would only be interested in spectral estimates up to and including 64Hz. The reason is that any sampled data above the Nyquist frequency is subject to aliasing. Essentially, rhythms in the data occurring above the Nyquist frequency are under-sampled: one has not got enough datum-points to represent the entire rhythmic cycle of such components. So, if we were to attempt to reconstructed the original signal from the sampled data, the rhythms above the Nyquist would be reconstructed at an incorrect frequency, i.e. they appear as something they are not, an alias. So, we truncate ![]() , removing all datum-points above the Nyquist frequency and denoted the new length as
, removing all datum-points above the Nyquist frequency and denoted the new length as ![]() :
:
|
|
(9) |
where the subscript T in ![]() denotes the truncated version of the DFT.
denotes the truncated version of the DFT.
In order to conserve power correspondence between time and frequency domains—owing to the fact that spectral estimates above the Nyquist frequency were discarded, ![]() will be multiplied by 2 over the range
will be multiplied by 2 over the range ![]() , where
, where ![]() is the DC-offset of the signal and
is the DC-offset of the signal and ![]() is the Nyquist frequency. For this particular estimate of the PSD, we compute a new window normalisation constant
is the Nyquist frequency. For this particular estimate of the PSD, we compute a new window normalisation constant ![]() :
:
|
|
(10) |
where ‘ denotes the vector transpose. In the case of a rectangular window W = 1 and can be substituted by window length L. In most practical instances, the scaled, normalised periodogram is taken as an estimate of the PSD:
|
|
(11) |
where the sampling interval ![]() ; the frequency index of each bin,
; the frequency index of each bin, ![]() , is given as,
, is given as, ![]() .
.
% compute power spectral density W = w*w'; % normalisation constant Vt = V(1:length(V)/2); % truncate DFT It = zeros(1,length(Vt)); % zeropadded buffer It(2:end-1) = 2*(1/Fs)*(abs(Vt(2:end-1)).^2/W); It(1) = 2*(1/Fs)*(abs(Vt(1)).^2/W); It(end) = 2*(1/Fs)*(abs(Vt(end)).^2/W);

Periodogram Averaging (Welch’s Periodogram)
Mentioned previously, for the purposes of spectral analysis using a DFT, ![]() will be segmented into
will be segmented into ![]() equal length, wide-sense stationary segments of length
equal length, wide-sense stationary segments of length ![]() —these maybe overlapping or not:
—these maybe overlapping or not:
|
|
(12) |
where ![]() ,
, ![]() and
and ![]() is the length of the signal. The parameter,
is the length of the signal. The parameter, ![]() , is a positive integer value. When
, is a positive integer value. When ![]() , the segments will overlap; when
, the segments will overlap; when ![]() , the segments are non-overlapping (contiguous). The subscript
, the segments are non-overlapping (contiguous). The subscript ![]() in
in ![]() , is the index of the segment,
, is the index of the segment, ![]() .
. ![]() is the total number of segments for which,
is the total number of segments for which, ![]() . Thus, assuming
. Thus, assuming ![]() then
then ![]() (Oppenheim and Schafer, 2010, p. 868).
(Oppenheim and Schafer, 2010, p. 868).
A windowed-DFT will be applied to each segment to yield an estimate, ![]() , computed as in Eq 11. The resultant local spectral estimates will be averaged to yield a final estimate:
, computed as in Eq 11. The resultant local spectral estimates will be averaged to yield a final estimate:
|
|
(13) |
% generate a signal (random noise) clear rng default% reset random number generator % signal Fs = 512; % sampling rate duration = 120; % 120 second duration signal Q = Fs * duration; x = 0 + 2.*randn(1,Q); % zero-mean random noise t = 0:1/Fs:duration-1/Fs; % time-index (2 seconds) x = cos(2*pi*100*t) + x; % sinusoidal at 100 Hz % segmentation parameters L = 1024; R = 1024; K = Q/L; F = (Fs/L)*(0:L-1); % frequency index in Hertz % compute periodogram [w] = compHamming(L); % hamming window PSDs = zeros(K,L/2); for r = 0:K-1 % window the signal startInd = (r*R)+1; endInd = (startInd+L)-1; xr = x(1,startInd:endInd); v = xr.*w; [It] = computeScaledPSD(v,w,Fs); % PSD PSDs(r+1,:) = It; end % average across segments estPSD = mean(PSDs,1);



Baseline Standardisation
The PSD is represented in log or linear scale, or as a baseline standardised measure: measured relative to a baseline or reference period. The latter is often expressed as a percentage change in power, a z-score, or a difference score taken between logarithmically-scaled spectral estimates. The choice is dependent upon the application (Delorme & Makeig, 2004; Gerhold, 2017; Klimesch, 1999; Pfurtscheller & Lopes da Silva, 1999). Baseline standardised EEG measurements are used extensively in consumer neuroscience applications
(see Vecchiato, Cherubino, Trettel & Bablioni, 2013 for detailed methodologies applied to television advertising assessments using many of the above-mentioned baseline standardisation methodologies). The reader may also consult Gerhold (2017, Ch2, p. 11-54), wherein the author(s) discuss the various trade-offs involved in parametrisation of the DFT algorithm for analysis of event-related EEG data.
Measures of Band-Power
As Parceval’s theorem holds (which is generally stated for a continuous case of the Fourier transform), integrating values between any two points on a frequency domain function will yield energy in a sub-band bounded by two points. In the case of a PSD, summing values bounded by two frequency points ![]() and
and ![]() yields total band-power in that sub-band:
yields total band-power in that sub-band:
|
|
(14) |
Alternatively, the values including and between the upper and lower bound may be averaged to provide average band-power, a ubiquitous measure of oscillatory power of an EEG signal:
|
|
(15) |
where ![]() is the total number of frequency bins summed across.
is the total number of frequency bins summed across.
% compute band power measures
f1 = 7.5; f2 = 13;
f1 = find(F==f1); f2 = find(F==f2);
totalBandPower = sum(10*log10(estPSD(1,f1:f2)));
J = (f2-f1)+1; avgBandPower = totalBandPower/J;
Electricity Reflects the Content of the Mind
Through studying the power of the EEG signals in different sub-bands and how these band-power measures covary with task demands, in terms of cognitive or affective processes, we can gain an understanding of how the human brain (specifically how the cerebral cortex) responds to and handles information and even make predictions about populations of participants and consumers. For pivotal methodological and theoretical literature, see Klimesch (1999) and Klimesch, Sauseng, & Hanslmayr (2007). For consumer neuroscience applications see Ramsøy, Skov, Christensen, & Stahlhut (2018), Shestyuk, Kasinathan, Karapoondinott, Knight, & Gurumoorthy (2019) and Vecchiato, Cherubino, Trettel, & Babiloni (2013).
Delorme, A., & Makeig, S. (2004). EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. Journal of Neuroscience Methods, 134, 9–21.
Gerhold, M. (2017). A study of event-related electrocortical oscillatory dynamics associated with cued motor-response inhibition during performance of the Go/NoGo task within a sample of prenatally alcohol-exposed children and age-matched controls. Cape Town: University of Cape Town.
Klimesch, W. (1999). EEG alpha and theta oscillations reflect cognitive and memory performance: a review and analysis. Brain Research Reviews, 29, 169–195.
Oppenheim, A. V., & Schafer, R. W. (2010). Discrete-Time Signal Processing (International Edition). Upper Saddle River: Pearson.
Pfurtscheller, G., & Lopes da Silva, F. H. (1999). Event-related EEG/MEG synchronization and desynchronization: basic principles. Clinical Neurophysiology, 110, 1842–1857.
Ramsøy, T. Z., Skov, M., Christensen, M. K., & Stahlhut, C. (2018). Frontal Brain Asymmetry and Willingness to Pay. Frontiers in Neuroscience, 12. https://doi.org/10.3389/fnins.2018.00138
Shestyuk, A. Y., Kasinathan, K., Karapoondinott, V., Knight, R. T., & Gurumoorthy, R. (2019). Individual EEG measures of attention, memory, and motivation predict population level TV viewership and Twitter engagement. PLOS ONE, 14, e0214507. https://doi.org/10.1371/journal.pone.0214507
Vecchiato, G., Cherubino, P., Trettel, A., & Babiloni, F. (2013). Neuroelectrical Brain Imaging Tools for the Study of the Efficacy of TV Advertising Stimuli and their Application to Neuromarketing. In Biosystems & Biorobotics. Retrieved from https://www.springer.com/gp/book/9783642380631

Published under: Consumer Neuroscience


![Rendered by QuickLaTeX.com \[ I_{PSD}[k]=\left\{\begin{array}{@{}ll@{}} 2 \triangle t\left(\frac{|V_T[k]|^2}{W}\right), & 1<k<M-1,\\ \;\, \triangle t\left(\frac{|V_T[k]|^2}{W}\right), & \text{otherwise}. \end{array}\right. \]](https://electricmind.me/wp-content/ql-cache/quicklatex.com-3f2381e86c65b5d3e82a65e8f69eb6be_l3.png)
![Rendered by QuickLaTeX.com \[ \hat{I}_{PSD}[F]=\frac{1}{K}\sum_{r=0}^{k-1}I_{PSD(r)}[F], \quad 0 \leq F \geq Nyquist. \]](https://electricmind.me/wp-content/ql-cache/quicklatex.com-797fe8c5b38087aa6ae1ecad41acbac2_l3.png)
![Rendered by QuickLaTeX.com \[ TotalBandPower=\sum_{F=f(1)}^{f(2)} \hat{I}_{PSD}[F]. \]](https://electricmind.me/wp-content/ql-cache/quicklatex.com-688014ee4204fd37e5e04e5b1efa2752_l3.png)
