This two-part series looks at the underlying mathematical theory and practical steps required to execute a spectral analysis of acquired electroencephalographic data. Spectral analysis, analysing how a signal’s power is distributed across a range of discrete frequencies, is fundamental to understanding an electroencephalogram as well as associated changes in psychological states. Solid, robust, replicable electrophysiology is built on the foundation of spectral analysis and one cannot emphasise enough the importance of the Fourier transform in this regard. The first part of this series deals with the general theory of the discrete Fourier transform (DFT), while the second part focuses on the mathematical/statistical properties of an EEG and how to apply a DFT in the context of biomedical signal-processing.
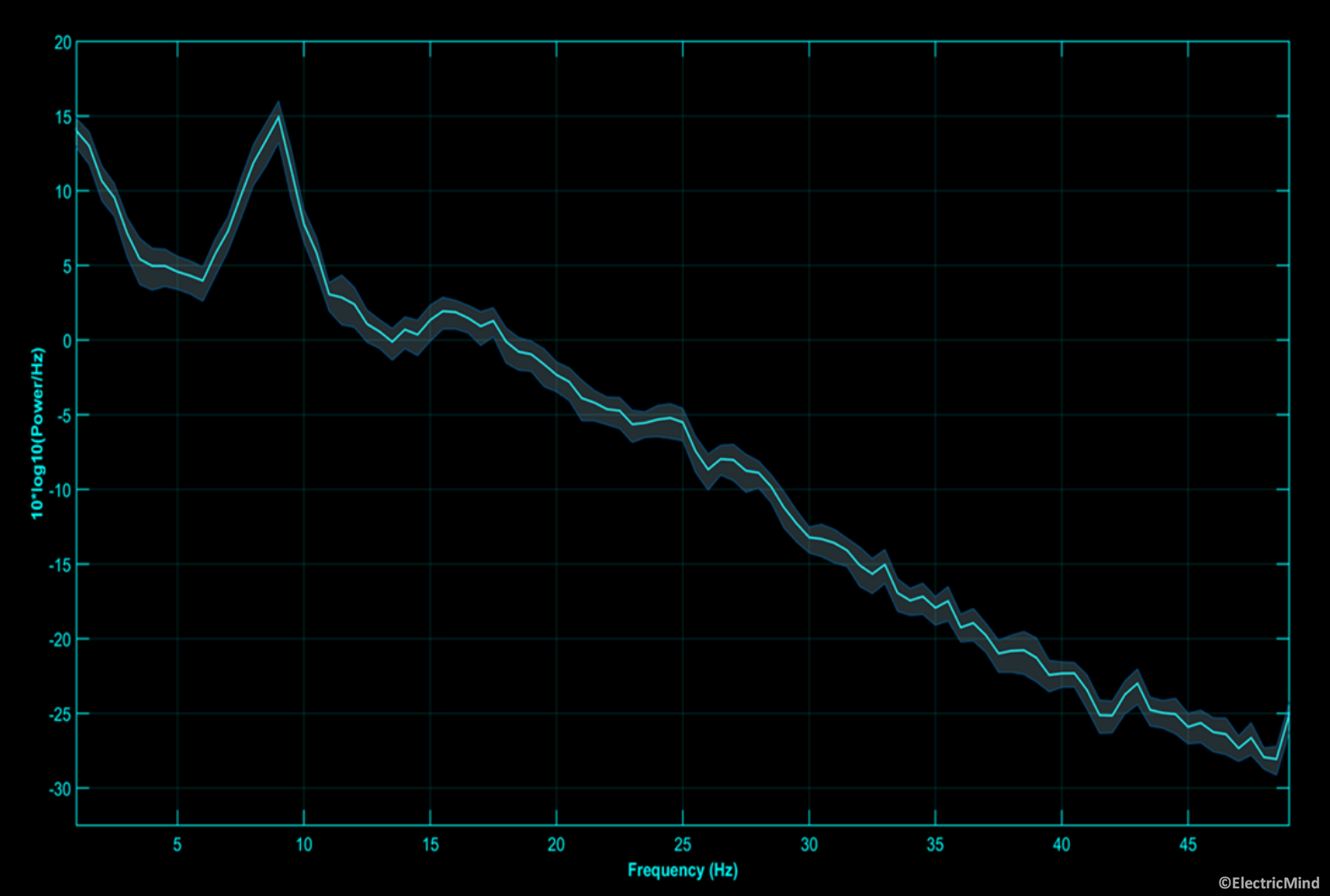
Power spectral density of an electroencephalographic signal recorded over the occipital region during an eyes-open session. The shaded area around the spectrum is the 95% confidence interval around the mean of the estimate. The spectra has a number of prominent rhythmic components. The strong peak at 9Hz is the dominant alpha rhythm. One can also observe a strong beta component from 13Hz-17Hz. Together, these spectral features indicate that the person is alert, awake, and aware of their environment.
The software used for this two-part series is available for download here. The documentation for the software may be viewed here.
EEG Analysis
The electroencephalogram can be analysed in several different ways. In diagnostic instances, a clinical specialist will visually review a recording, looking for visible changes in the signals, in order to identify bioelectrical abnormalities associated with disease. For example, the aberrant electro-cortical activity associated with epilepsy, referred to as ictal activity, can be visually identified in an EEG (Beal et al., 2018; Krishnan, Chang, & Schomer, 2017; Spinosa, Liberalesso, Mehl, & Löhr Júnior, 2011).
Using information in the EEG that may not necessarily be amenable to visual analysis, certain disorders may also be distinguished from others. The electro-cortical features that point to a disease, cognitive and/or emotional abnormalities are known as biomarkers (Nicotera et al., 2019; Smailovic et al., 2018; Snyder, Rugino, Hornig, & Stein, 2015). These features of an EEG signal are extracted using engineering-based methodologies to undercover the information “hidden” from visual inspection (Delorme & Makeig, 2004; Oostenveld, Fries, Maris, & Schoffelen, 2011). Biomarkers can also be used to measure cognitive processes that unfold in real-time (Freeman, Mikulka, Prinzel, & Scerbo, 1999; McMahan, Parberry, & Parsons, 2015).
The discrete Fourier transform
EEG analysis rests on the foundations of digital-signal processing methodologies (Delorme & Makeig, 2004; Klimesch, 1999; Oostenveld et al., 2011; Pfurtscheller & Lopes da Silva, 1999; Sanei & Chambers, 2007). The most important of all of signal-processing methods is the Fourier transform. The Fourier transform, specifically the discrete Fourier transform (DFT), is used to transform a digitally-sampled signal into a representation that allows one to assess the strength of the signal’s periodicities (rhythmic components) distributed as a function of frequency.
Analytically, this transform decomposes the time-domain signal into a sum of sinusoidal waves at discrete frequencies. From this sinusoidal representation, we can analyse the structure of the time-domain signal. Thus, we can talk about the spectral content of a signal or its spectrum. Alternatively, we can talk about transforming the signal into the frequency-domain (for an in-depth discussion see: Oppenheim and Schafer, 2010, Ch 8 p. 648 – 741).
The equation below is the DFT for a finite-length signal ![]() of length
of length ![]() :
:
|
|
(1) |
where ![]() , a complex-exponential representation of the basic sinusoidal functions (sine and cosine) that the signal will be decomposed into. The values of
, a complex-exponential representation of the basic sinusoidal functions (sine and cosine) that the signal will be decomposed into. The values of ![]() contain information about the combination of sinusoidal waves required to build the time domain signal
contain information about the combination of sinusoidal waves required to build the time domain signal ![]() , this information includes magnitude as well as phase information.
, this information includes magnitude as well as phase information.
The inverse transform from frequency-domain back to the time-domain is given by:
|
|
(2) |
(Oppenheim and Schafer, 2010, p. 744).
The DFT is implemented in a number of different computational algorithms: Goertzel’s algorithm, the Winograd Fourier transform, and the fast Fourier transforms (FFT). As the name indicates, FFT algorithms exploit the essential properties of the Fourier transform in order to expeditiously compute ![]() .
.
Parceval’s theorem
According to Parceval’s theorem, the signal’s energy within the time-domain is conserved in the transformation into the frequency domain representation (Oppenheim & Schafer, 2010, p. 88). Thus, for a finite-length, discrete signal:
|
|
(3) |
where ![]() is the DFT of the signal
is the DFT of the signal ![]() .
.
Parceval’s theorem is generally stated from a continuous case using integrals of trigonometric functions, where frequency is represented as a continuous variable, time may be continuous or discrete. In comparison to a digital signal, where time and frequency are both always discrete and summation is used instead of integration. Thus, when evaluating Eq 3 on a digital signal, we find Eq 3 is true to a certain level of precision, this results from rounding and sampling of the digital representation of the signal.
The periodogram
The frequency domain representation, ![]() , is often expressed as a power spectral estimate: signal power varying as a discrete function of frequency. The power spectrum is an estimated quantity, representative of the true power spectrum of the underlying data-generating process
, is often expressed as a power spectral estimate: signal power varying as a discrete function of frequency. The power spectrum is an estimated quantity, representative of the true power spectrum of the underlying data-generating process ![]() , where
, where ![]() denotes the power spectrum, and subscript
denotes the power spectrum, and subscript ![]() the signal.
the signal. ![]() is sampled at discrete frequencies,
is sampled at discrete frequencies, ![]() , where
, where ![]() . For periodic phenomena occurring in nature,
. For periodic phenomena occurring in nature, ![]() is always continuous. The act of observing the signal through digitisation and applying signal-processing methods, means that we sample the naturally-occuring, continuous frequency-spectrum at discrete points.
is always continuous. The act of observing the signal through digitisation and applying signal-processing methods, means that we sample the naturally-occuring, continuous frequency-spectrum at discrete points.
The power spectral estimate is also referred to as the periodogram, herein denoted as ![]() . Some important properties of
. Some important properties of ![]() are: non-negative for real-valued signals; a real-valued function of frequency, and an even function of frequency (this property refers to the symmetric nature of the function, i.e. the function is mirrored at a midpoint of the estimate).
are: non-negative for real-valued signals; a real-valued function of frequency, and an even function of frequency (this property refers to the symmetric nature of the function, i.e. the function is mirrored at a midpoint of the estimate).
There is some fairly deep mathematical theory behind how the periodogram is derived, as well as its relationship to the true power spectrum of the data-generating process, which we will not go into detail for simplicities sake. Herein, we focus on the instance of the DFT used in the context of EEG signal-processing, providing the essential theory to enable EEG signal-processing pipelines. Here we address the periodogram in general and later-on in the series focus on a specific application to EEG signals.
Windowing
In digital-signal processing applications, an acquired signal, ![]() , will be windowed: prior to computing the DFT, the signal will be multiplied by a windowing (tapering) function,
, will be windowed: prior to computing the DFT, the signal will be multiplied by a windowing (tapering) function, ![]() , the length of which is denoted
, the length of which is denoted ![]() . We denote the windowed signal
. We denote the windowed signal ![]() :
:
|
|
(4) |
In this section, we assume that the window length is the same as the length of the signal, ![]() , and that
, and that ![]() is even.
is even.
Characteristically, EEG spectral analysis—estimating the periodogram and examining its properties—makes use of Gaussian-shaped (cosine-sum) functions, such as the Hamming window:
|
|
(5) |
(Oppenheim and Schafer, 2010, p. 565-566). Note: for the purposes of spectral analysis, the window is computed at length ![]() and last sample point discarded, this is known as a periodic window (ibid. p. 566).
and last sample point discarded, this is known as a periodic window (ibid. p. 566).
The window function, ![]() , effectively weights-down (smooths) values at the start and end of the segment
, effectively weights-down (smooths) values at the start and end of the segment ![]() , less so in the middle—with the exception of a rectangular window, where all sample points are given equal weighting:
, less so in the middle—with the exception of a rectangular window, where all sample points are given equal weighting: ![]() . The periodogram estimated using a rectangular window is known simply as the periodogram, while an estimate using a non-rectangular window is known as the modified periodogram.
. The periodogram estimated using a rectangular window is known simply as the periodogram, while an estimate using a non-rectangular window is known as the modified periodogram.
Non-rectangular windows reduce spectral leakage, a methodological phenomenon where component power is attributed to neighbouring frequency components within the periodogram—this is also referred to as sidelobe leakage.
% generate a signal (random noise) x = 0 + 2.*randn(1,1024); N = length(x); L = N; % compute a periodic hamming window function w = zeros(); for n = 1:L+1 w(n) = 0.54-0.46*cos(2*pi*(n/L)); end w(end) = []; % window the signal v = x.*w;

The Leakage Effect
There are two main explanations why leakage occurs. Firstly, the DFT requires that all frequency components are periodic within the window with an integral number of periods: they complete full cycles within the window. It is inevitable that real-world signals are going to have frequency components that don’t fit this criterion, and it’s not possible to adjust the window length to accommodate for this: some components will only complete partial cycles towards the end of the window. The DFT computation resolves the power of these components into adjacent frequency bins, i.e. the power “leaks”.
The second explanation is that, simply by segmenting the signal, it can be proven that mathematical operations are implicitly applied in the frequency domain. This means that the DFT we observe, is a result of the spectral characteristics of the signal combined (convolved) with the spectral characteristics of the window function—even if the segmented signal is not explicitly windowed, as in the case of ![]() , this implicit computation occurs. Due to the shape of the DFT of the window function, all frequency bins receive power from all other bins: power from a single frequency bin “leaks” across the spectrum. The shape of the DFT of the window function determines how the frequency bins are connected, thus the extent of the leakage effect. Cosine windows do well to reduce this effect.
, this implicit computation occurs. Due to the shape of the DFT of the window function, all frequency bins receive power from all other bins: power from a single frequency bin “leaks” across the spectrum. The shape of the DFT of the window function determines how the frequency bins are connected, thus the extent of the leakage effect. Cosine windows do well to reduce this effect.
With a reduction in leakage comes an accompanying decrease in frequency resolution. What this means is that a narrow frequency component of say 1Hz band-width will be distributed more widely across frequency, but the extent to which power leaks is greatly reduced. So, at a relatively high resolution, this component may appear thin and concentrated, while at lower resolutions, the component will be fatter and spread more widely across the frequency bins; the peak of the component will also be lower. These changes in resolution can affect our ability to distinguish two closely-spaced frequency components, as components are blurred into each other; in engineering parlance, our ability to resolve closely spaced components is affected.
Normalisation/Scaling
When using different window types (hamming vs. rectangular) in finite, small-samples, one will observe a change in the average power of the spectral estimate owing to the different relative weightings applied to each sample point of the windowed signal. When the signal lengths approaches infinity (a theoretical concept), the estimates will be biased. Therefore, the power estimate will be scaled with a window normalisation constant, ![]() , multiplied by segment length
, multiplied by segment length ![]() . This ensures equivalent average power for PSD estimates under asymptotic assumptions, regardless of window type used, i.e. for all window types, the bias of the estimate will converge to zero as
. This ensures equivalent average power for PSD estimates under asymptotic assumptions, regardless of window type used, i.e. for all window types, the bias of the estimate will converge to zero as ![]() :
:
|
|
(6) |
(Oppenheim and Schafer, 2010, p. 865).
In the instance of a rectangular window, ![]() , otherwise window types yield a value where
, otherwise window types yield a value where ![]() . Thus, assuming a modified periodogram, using a hamming window defined in Eq 5, the DFT of the windowed signal is:
. Thus, assuming a modified periodogram, using a hamming window defined in Eq 5, the DFT of the windowed signal is:
|
|
(7) |
The periodogram is defined as:
|
|
(8) |
where the frequency index of the ![]() bin is given as,
bin is given as, ![]() .
.
% compute the periodogram estimate Fs = 512; % sampling rate in Hertz V = fft(v); % compute the DFT via an FFT U = sum(w.^2)/L; % compute window normalisation constant I = (abs(V).^2)/(L*U); % periodogram F = (Fs/L)*(0:L-1); % frequency index in Hertz

Properties of the Periodogram
The periodogram is an estimate of the underlying data-generating process’s power spectrum ![]() within a range defined by
within a range defined by ![]() , where
, where ![]() is discrete. In the instance of the brain, the periodogram is an estimate of an electro-cortical process’s true power spectral density under specific experimental conditions. The periodogram is known to be a biased estimate when estimated from finite length signals; however, a modified periodogram estimate, using appropriate scaling and normalisation, will be unbiased as N approaches infinity: it is an asymptotically unbiased estimate, therefore
is discrete. In the instance of the brain, the periodogram is an estimate of an electro-cortical process’s true power spectral density under specific experimental conditions. The periodogram is known to be a biased estimate when estimated from finite length signals; however, a modified periodogram estimate, using appropriate scaling and normalisation, will be unbiased as N approaches infinity: it is an asymptotically unbiased estimate, therefore ![]() as
as ![]() , where the operator
, where the operator ![]() denotes the expected mean.
denotes the expected mean.
The periodogram, however, is an inconsistent estimate, i.e. the variance does not converge to zero as N approaches infinity. For large N, ![]() . In order, to address this, the periodogram routine introduces averaging over signal segments, which has the effect of decreasing the variance of the periodogram. The estimate becomes consistent, i.e. it converges to zero as the number of statistically independent segments approaches infinity:
. In order, to address this, the periodogram routine introduces averaging over signal segments, which has the effect of decreasing the variance of the periodogram. The estimate becomes consistent, i.e. it converges to zero as the number of statistically independent segments approaches infinity: ![]() as
as ![]() . However, this decrease in variance trades-off with a corresponding increase in estimation bias: a bias-variance trade-off takes place. This important and pivotal trade-off will be clearly illustrated as we proceed in this series of articles.
. However, this decrease in variance trades-off with a corresponding increase in estimation bias: a bias-variance trade-off takes place. This important and pivotal trade-off will be clearly illustrated as we proceed in this series of articles.
Periodogram estimation and averaging in the context of EEG signals are covered in Part 2 of this series.
Beal, J. C., Eisermann, M., Misra, S. N., Pearl, P. L., Plouin, P., Mizrahi, E. M., & Sl, M. (2018). Seizures and Epilepsy in Preterm and term neonates, infants, children and adolescents,. Niedermeyer’s Electroencephalography Seventh Edition. Retrieved from https://www.scholars.northwestern.edu/en/publications/seizures-and-epilepsy-in-preterm-and-termneonates-infants-childre…
Delorme, A., & Makeig, S. (2004). EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. Journal of Neuroscience Methods, 134, 9–21.
Freeman, F. G., Mikulka, P. J., Prinzel, L. J., & Scerbo, M. W. (1999). Evaluation of an adaptive automation system using three EEG indices with a visual tracking task. Biological Psychology, 50, 61–76.
Klimesch, W. (1999). EEG alpha and theta oscillations reflect cognitive and memory performance: a review and analysis. Brain Research Reviews, 29, 169–195.
Krishnan, V., Chang, B. S., & Schomer, D. L. (2017). The Application of EEG to Epilepsy in Adults and the Elderly. Retrieved from http://oxfordmedicine.com/view/10.1093/med/9780190228484.001.0001/med-9780190228484-chapter-19
McMahan, T., Parberry, I., & Parsons, T. D. (2015). Evaluating Player Task Engagement and Arousal Using Electroencephalography. Procedia Manufacturing, 3, 2303–2310. https://doi.org/10.1016/j.promfg.2015.07.376
Nicotera, A. G., Hagerman, R. J., Catania, M. V., Buono, S., Di Nuovo, S., Liprino, E. M., … Musumeci, S. A. (2019). EEG Abnormalities as a Neurophysiological Biomarker of Severity in Autism Spectrum Disorder: A Pilot Cohort Study. Journal of Autism and Developmental Disorders. https://doi.org/10.1007/s10803-019-03908-2
Oostenveld, R., Fries, P., Maris, E., & Schoffelen, J. M. (2011). FieldTrip: Open Source Software for Advanced Analysis of MEG, EEG, and Invasive Electrophysiological Data. Computational Intelligence and Neuroscience. https://doi.org/10.1155/2011/156869
Oppenheim, A. V., & Schafer, R. W. (2010). Discrete-Time Signal Processing (International Edition). Upper Saddle River: Pearson.
Pfurtscheller, G., & Lopes da Silva, F. H. (1999). Event-related EEG/MEG synchronization and desynchronization: basic principles. Clinical Neurophysiology, 110, 1842–1857.
Sanei, S., & Chambers, J. A. (2007). EEG Signal Processing. Retrieved from https://www.wiley.com/en-us/EEG+Signal+Processing-p-9780470025819
Smailovic, U., Koenig, T., Kåreholt, I., Andersson, T., Kramberger, M. G., Winblad, B., & Jelic, V. (2018). Quantitative EEG power and synchronization correlate with Alzheimer’s disease CSF biomarkers. Neurobiology of Aging, 63, 88–95.
Snyder, S. M., Rugino, T. A., Hornig, M., & Stein, M. A. (2015). Integration of an EEG biomarker with a clinician’s ADHD evaluation. Brain and Behavior, 5(4), e00330. https://doi.org/10.1002/brb3.330
Spinosa, M. J., Liberalesso, P. B., Mehl, L., & Löhr Júnior, A. (2011). Ictal patterns in children: an illustrated review. Journal of Epilepsy and Clinical Neurophysiology, 17, 154–163. https://doi.org/10.1590/S1676-26492011000400008

Published under: Consumer Neuroscience


![Rendered by QuickLaTeX.com \[ X[k]=\sum_{n=0}^{N-1}{x[n]W\frac{kn}{N}},\quad k = 0, 1,\dots,N-1, \]](https://electricmind.me/wp-content/ql-cache/quicklatex.com-e6e3ada80bd24234683d4c5a86c6e51a_l3.png)
![Rendered by QuickLaTeX.com \[ X[n] = \frac{1}{N}\sum_{k=1}^{N-1}X[k]W\frac{-kn}{N},\quad n = 0, 1,\dots,N-1, \]](https://electricmind.me/wp-content/ql-cache/quicklatex.com-0eff3a815823f2d8ce8d2e2ae9c7e689_l3.png)
![Rendered by QuickLaTeX.com \[ \sum_{n=0}^{N-1}|x[n]|^2 = \frac{1}{N}\sum_{k=0}^{N-1}|X[k]|^2, \]](https://electricmind.me/wp-content/ql-cache/quicklatex.com-8d90614aadc4debb7bc6c43ee9ad339d_l3.png)
![Rendered by QuickLaTeX.com \[ U = \frac{1}{L}\sum_{n=0}^{L-1}w[n]^2 \]](https://electricmind.me/wp-content/ql-cache/quicklatex.com-db1c456b16c0e2fbd5c034dab2eaf9a0_l3.png)
![Rendered by QuickLaTeX.com \[ V[k]=\sum_{n=0}^{N-1}v[k]W\frac{kn}{N},\quad k = 0,1,\dots,L-1. \]](https://electricmind.me/wp-content/ql-cache/quicklatex.com-568bb866796bafa23da3dc6013ded7b9_l3.png)
